文章轉載出處:親子天下 翻轉教育
響尾蛇的數學天地
最後通牒遊戲,你的選擇是?
假設有人出100塊錢,給你和另外一個不認識的人去分,只要你們兩人都同意怎麼分這筆錢,就可以把錢拿走。但是,你們必須遵守嚴格的規定。兩個人必須分別待在不同的房間,不能交談或溝通。一開始,先擲銅板決定誰有權提議如何分錢,假定你取得了建議權,你只會有一次提議的機會,而另外一個人也只有一次機會回答「同意」或「不同意」。對方和你一樣,很清楚遊戲規則和現金總額,如果他同意你的提議,你們就可以分掉這筆錢;如果他不同意,你們兩個人就一文錢都拿不到。無論結果如何,遊戲都到此結束,不會再重來一遍。在這種情況下,你會怎麼辦呢?
響尾蛇的數學天地
最後通牒遊戲,你的選擇是?
假設有人出100塊錢,給你和另外一個不認識的人去分,只要你們兩人都同意怎麼分這筆錢,就可以把錢拿走。但是,你們必須遵守嚴格的規定。兩個人必須分別待在不同的房間,不能交談或溝通。一開始,先擲銅板決定誰有權提議如何分錢,假定你取得了建議權,你只會有一次提議的機會,而另外一個人也只有一次機會回答「同意」或「不同意」。對方和你一樣,很清楚遊戲規則和現金總額,如果他同意你的提議,你們就可以分掉這筆錢;如果他不同意,你們兩個人就一文錢都拿不到。無論結果如何,遊戲都到此結束,不會再重來一遍。在這種情況下,你會怎麼辦呢?
「最後通牒」其實是心理學家設計 來質疑賽局專家的一種遊戲,這個實驗的結果超乎一 般賽局學者的預期,如果膽敢只十分之一給對手,幾 乎都會遭到兩敗俱傷的拒絕,不會有什麼十元總比零 元好的「納許均衡」,自以為聰明的算計,常因氣氛 不好味道不對而破局,所以是負面的「心理報償」。
「博奕理論」(game theory)是種形式方法,用來分析決策人員之間的競爭或合作互動,對棋局或整體社會都適用。先從簡單的開始,我們可以從普通遊戲(如井字遊戲或西洋棋),得到一些賽局的通則,這類賽局擁有完全資訊,因為所有參賽者都知道規則、可能選擇和遊戲歷史。這表示參賽者可以對賽局有全盤計畫,能掌握特定的應對方式來應付賽局中任何可能事件,以純策略贏得賽局。但是,像剪刀石頭布或撲克牌這類非完全資訊的賽局,就沒有保證獲勝的純策略。如果玩家太常運用某種策略,就會被其對手識破利用。這類賽局就是現代數學博奕理論派上用場的地方,能針對最佳混合策略與勝局期望頻率,提出洞見。
「博奕理論」(game theory)是種形式方法,用來分析決策人員之間的競爭或合作互動,對棋局或整體社會都適用。先從簡單的開始,我們可以從普通遊戲(如井字遊戲或西洋棋),得到一些賽局的通則,這類賽局擁有完全資訊,因為所有參賽者都知道規則、可能選擇和遊戲歷史。這表示參賽者可以對賽局有全盤計畫,能掌握特定的應對方式來應付賽局中任何可能事件,以純策略贏得賽局。但是,像剪刀石頭布或撲克牌這類非完全資訊的賽局,就沒有保證獲勝的純策略。如果玩家太常運用某種策略,就會被其對手識破利用。這類賽局就是現代數學博奕理論派上用場的地方,能針對最佳混合策略與勝局期望頻率,提出洞見。
Nash均衡(Nash equilibrium)是賽局理論中一個很重要的概念。如果某一組策略是Nash均衡,任何一個參賽者單獨改變自己的策略並不會使自己的報酬提高。也就是說,如果別人都玩Nash均衡策略時,我會發現這個均衡策略會是我的最佳的選擇(也就是最適回應,best response)。當所有人都玩這一個Nash均衡策略時,沒有人會想要悖離(deviate)。
Nash均衡是基於某些對人的行為的假設。例如,所有參賽人皆清楚的了解對手有哪些行動,並且就所有可能的行動中選出一個最適的反應。而這些都是所有人的共同知識(common knowledge), 我們可以用以下的「囚犯困境」賽局來說明如何找出Nash均衡。
【賽局理論小遊戲 囚犯困境】
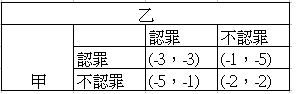
甲,乙兩人因案被捕,警方分開偵訊。因為證據不夠充分,須要嫌犯的自白。因此,警方告訴兩人,「如果你認罪,但你的同夥不認罪,你只要被關一年,但你的同夥要被關五年。可是如果你不認罪,而你的同夥認罪了,你要被關五年,但你的同夥只要被關一年。如果你們倆都認罪了,你們都要被關三年。」但如果兩人都不認罪,由於證據薄弱,兩人只要被關兩年。
Nash均衡是基於某些對人的行為的假設。例如,所有參賽人皆清楚的了解對手有哪些行動,並且就所有可能的行動中選出一個最適的反應。而這些都是所有人的共同知識(common knowledge), 我們可以用以下的「囚犯困境」賽局來說明如何找出Nash均衡。
【賽局理論小遊戲 囚犯困境】
甲,乙兩人因案被捕,警方分開偵訊。因為證據不夠充分,須要嫌犯的自白。因此,警方告訴兩人,「如果你認罪,但你的同夥不認罪,你只要被關一年,但你的同夥要被關五年。可是如果你不認罪,而你的同夥認罪了,你要被關五年,但你的同夥只要被關一年。如果你們倆都認罪了,你們都要被關三年。」但如果兩人都不認罪,由於證據薄弱,兩人只要被關兩年。
如果囚犯是自私的,他應該會選擇自己認罪,並希望對方不認罪;不過對方很可能也是自私的,所以容易導致兩人都認罪而形成(-3,-3)。兩人都依照檢察官的條件而認罪,並且都減刑至3年,似乎很合理。但仔細想想,這件事其實有蹊蹺。如果兩人都不認罪,形成的是(-2,-2),這絕對比(-3,-3)來得好!
問題就出在於,兩個囚犯都無法控制對方的意志,因此很容易陷在(-3,-3)當中。這個(-3,-3)就是所謂的納許均衡:「雙方已選定策略,在另一方不動的情形下,任一方改變策略並無法得到好處。此時的策略搭配後續結果,就構成納許均衡。」這裡雙方選定的策略就是「認罪」,而在另一方不動的情形下,任一方改為「不認罪」,只會讓自己的刑期變為五年,無法獲得好處;只有兩人都改為「不認罪」,才能讓兩人的刑期同時減至兩年。難以逃脫納許均衡的原因,就是雙方都無法確保對方將策略改為「不認罪」。
Nash均衡 (Nash equilibrium)
問題就出在於,兩個囚犯都無法控制對方的意志,因此很容易陷在(-3,-3)當中。這個(-3,-3)就是所謂的納許均衡:「雙方已選定策略,在另一方不動的情形下,任一方改變策略並無法得到好處。此時的策略搭配後續結果,就構成納許均衡。」這裡雙方選定的策略就是「認罪」,而在另一方不動的情形下,任一方改為「不認罪」,只會讓自己的刑期變為五年,無法獲得好處;只有兩人都改為「不認罪」,才能讓兩人的刑期同時減至兩年。難以逃脫納許均衡的原因,就是雙方都無法確保對方將策略改為「不認罪」。
Nash均衡 (Nash equilibrium)
【賽局理論小遊戲 決定一到一百的數字】
參加的同學只能決定一到一百的數字, 把數字的總和作一個平均,而數字最接近平均的一半的人為贏家.
遊戲流程
教師統一說明題目
『同學決定一到一百的數字, 把數字的總合作一個平均,而數字最接近平均的一半的人為贏家.』
以排為單位,排頭去計算排的平均
教師黑板寫
排號碼/
排平均/
排平均之半/
最接近排平均之半同學名字/
最接近排平均之半之數據/
勝利同學上台分享為何選這數字/
分發勝利獎品/
遊戲執行第二輪
教師黑板寫下
排號碼/
排平均/
排平均之半/
最接近排平均之半同學名字/
最接近排平均之半之數據/
分析數字收斂情形
....
參加的同學只能決定一到一百的數字, 把數字的總和作一個平均,而數字最接近平均的一半的人為贏家.
遊戲流程
教師統一說明題目
『同學決定一到一百的數字, 把數字的總合作一個平均,而數字最接近平均的一半的人為贏家.』
以排為單位,排頭去計算排的平均
教師黑板寫
排號碼/
排平均/
排平均之半/
最接近排平均之半同學名字/
最接近排平均之半之數據/
勝利同學上台分享為何選這數字/
分發勝利獎品/
遊戲執行第二輪
教師黑板寫下
排號碼/
排平均/
排平均之半/
最接近排平均之半同學名字/
最接近排平均之半之數據/
分析數字收斂情形
....
【分析】
所以假設平均為五十,一半就是二十五,數字最接近二十五的同學為贏家! 第一次玩的結果,平均是25.16,一半則是15.58....第二次玩的時候平均是19.8,一半則是9.9. 第三次玩的時候平均是9.107,一半則是4.5535.
有趣的是....這次的平均值是七點五,一半是三點七五....這個遊戲的最終答案是零....
所以假設平均為五十,一半就是二十五,數字最接近二十五的同學為贏家! 第一次玩的結果,平均是25.16,一半則是15.58....第二次玩的時候平均是19.8,一半則是9.9. 第三次玩的時候平均是9.107,一半則是4.5535.
有趣的是....這次的平均值是七點五,一半是三點七五....這個遊戲的最終答案是零....
【賽局理論小遊戲 撿紅點匹配】
讓全班的同學在紙上寫下一到十之中的任何一個數字,然後跟另外一位同學配對,如果數字和剛好等於十的倍數,兩個人就可以得到獎品。
讓全班的同學在紙上寫下一到十之中的任何一個數字,然後跟另外一位同學配對,如果數字和剛好等於十的倍數,兩個人就可以得到獎品。
國三會考後深化問題:請問配成對的機率為多少?
活動花絮


















 RSS 訂閱
RSS 訂閱